Transformers: Attention in Disguise

In this post, we will be describing a class of sequence processing models known as Transformers (…robots in disguise). Jokes aside, Transformers came out on the scene not too long ago and have rocked the natural language processing community because of their pitch: state-of-the-art and efficient sequence processing without recurrent units or convolution.

“No recurrent units or convolution?! What are these models even made of?!”, you may be exclaiming to unsuspecting strangers on the streets.

Not much it turns out, other than a bunch of attention and feedforward operations.

While the individual components that make up the Transformer model are not particularly novel, this is still a pretty dense paper with a lot of moving parts. So our aim in this post will be to distill the model to its key contributions, without getting too stuck in the details.

But first, the TLDR for the paper:

1. Transformers demonstrate that recurrence and convolution are not essential for building high-performance natural language models
2. They achieve state-of-the-art machine translation results using a self-attention operation
3. Attention is a highly-efficient operation due to its parallelizability and runtime characteristics

If that sounds exciting, read onward!

How Transformers Work

While the Transformer does not use traditional recurrent units or convolutions, it still takes inspiration from sequence-to-sequence architectures where we encode some input and iteratively decode a desired output.

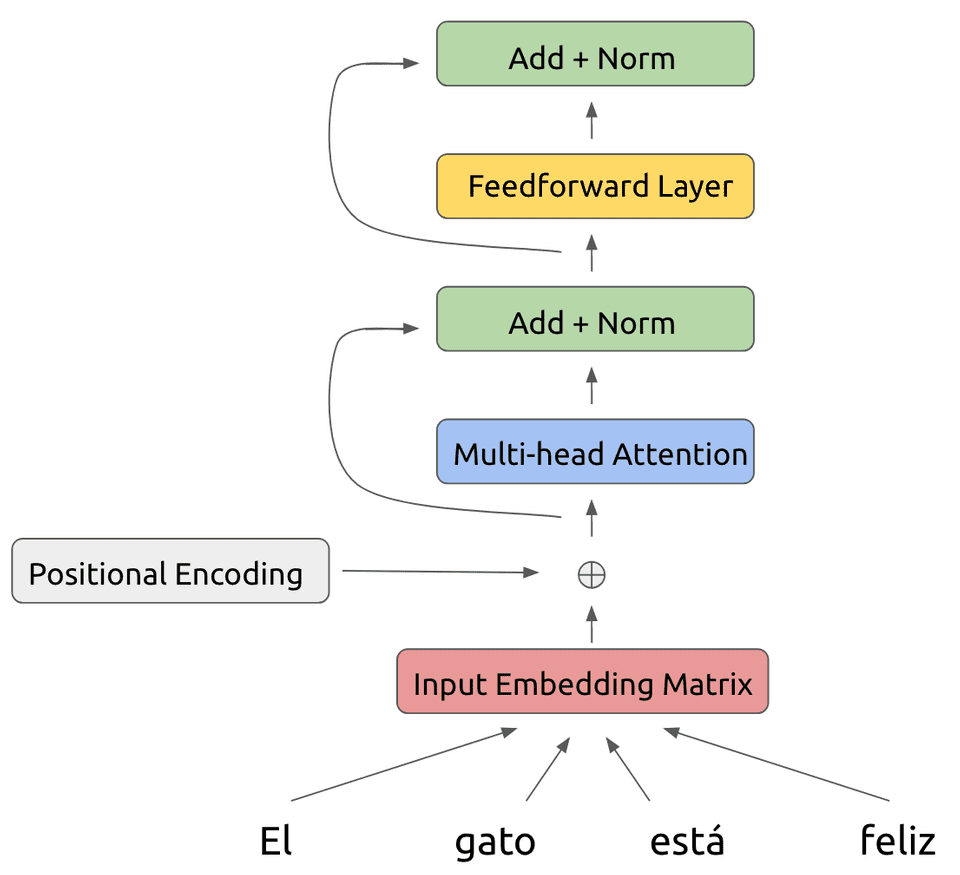
How does this play out in practice? Let’s focus on the encoder first. There are quite a few elements to the process, so don’t get too lost in the details. All we are doing is encoding some inputs 🙂.

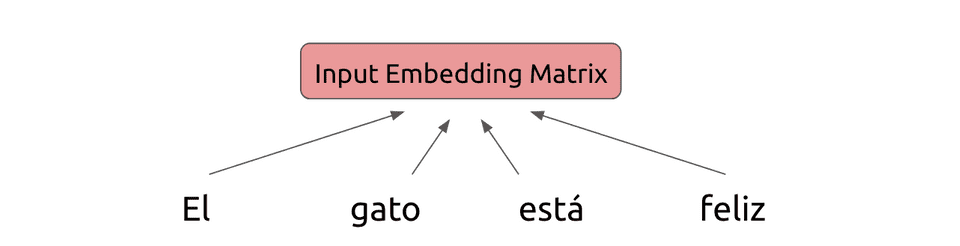
Assume we start with a certain phrase that we would like to translate from Spanish to English. The Transformer begins by embedding the tokens of the Spanish phrase into a conventional embedding matrix:

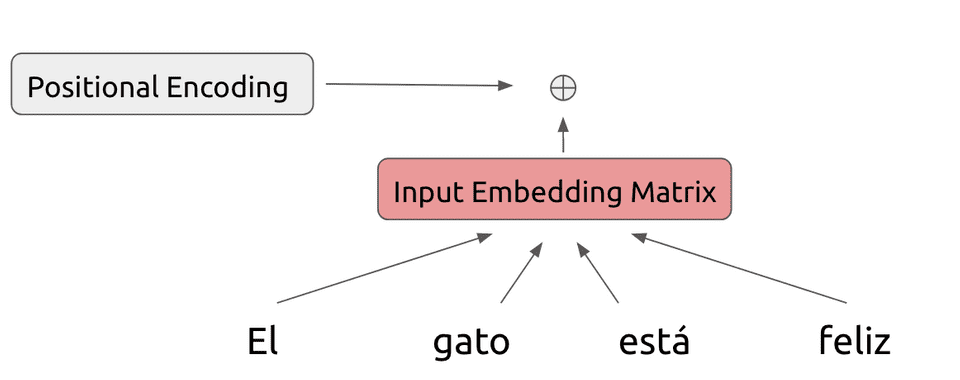
Because the model makes no use of recurrence, we need some way to represent position-based information in the model. Hence we add a positional encoding to this embedding matrix, whose exact form we will describe in the next section:

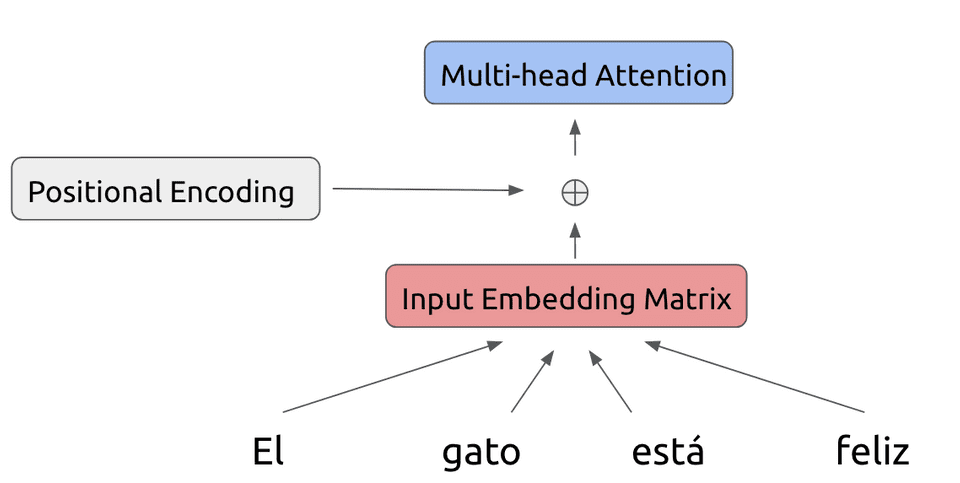
Our modified input is fed into the first layer of the Transformer encoder. Within each encoder layer, we perform a series of operations on the inputs.

First off, we feed the input through a multi-head attention operation:

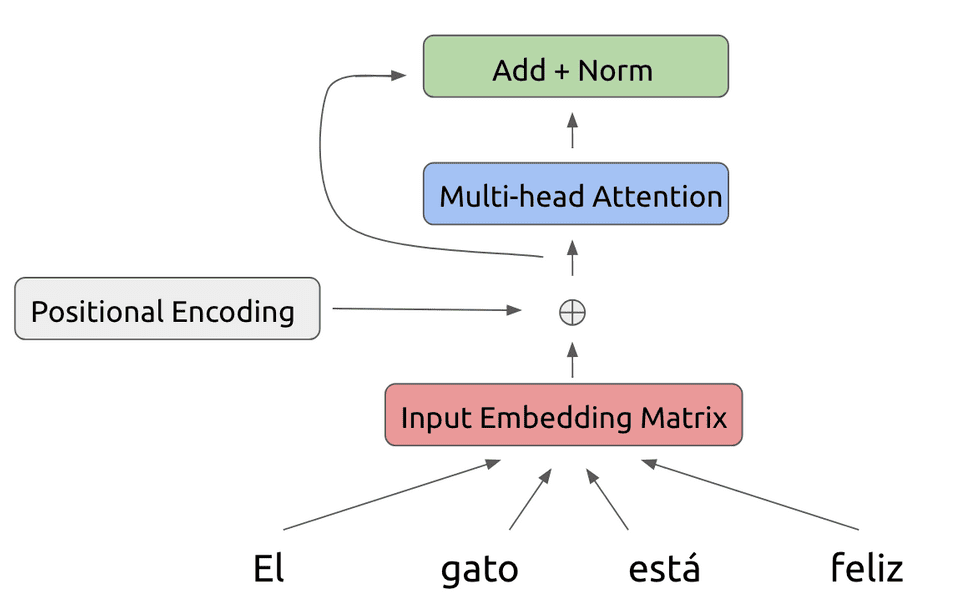
To this attention output, we also add a residual connection as well as perform a layer normalization step:

Now, we feed this result into a feedforward layer also using a residual connection and layer normalization:

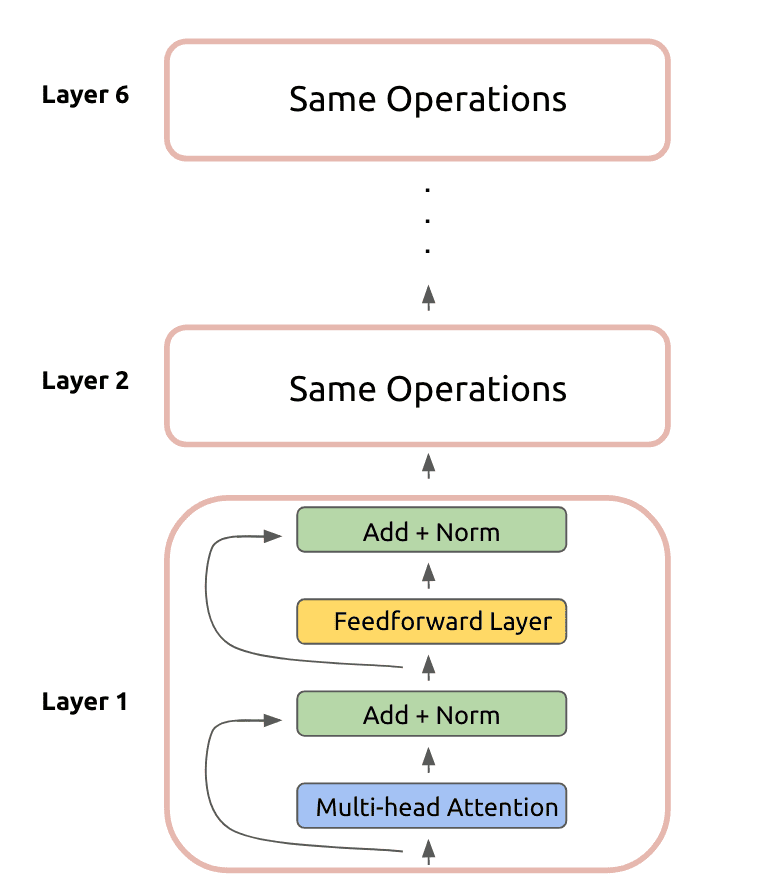
This is the result of our first layer encoder operation! This is fed as the input to another identical layer. In total, the Transformer encoder uses six stacked layers:

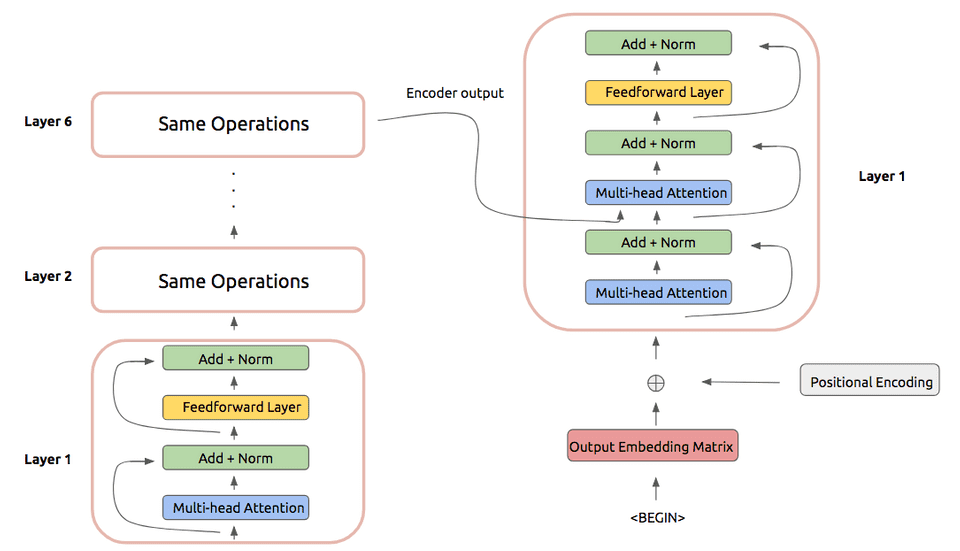
Now we can move on to the Transformer decoder. In practice, the decoder also uses six stacked layers that perform a set of operations. These operations are largely identical to the encoder layer, except for a few small differences:

• The first multi-head attention is a masked attention operation, where positions after the one being considered are not included in the attention computation
• Another multi-headed attention operation is included that has the decoder inputs attend over the output of the encoder stack. This operation takes inspiration from traditional recurrent sequence-to-sequence models.

In practice this look as follows:

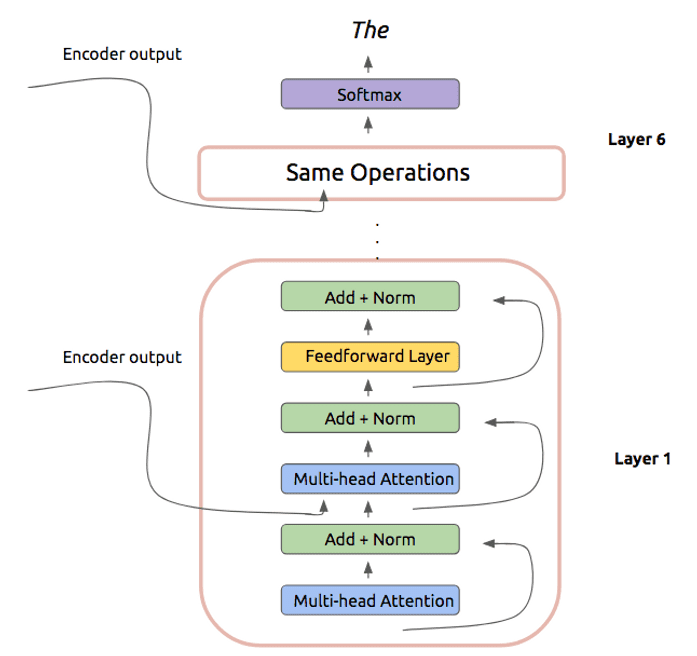
After performing these operations, we can predict the next token of our translated phrase:

And that’s the Transformer!

How Transformers Are Built

While the Transformer architecture may seem conceptually simple, the devil is of course in the details. To that end, there are quite a few aspects that warrant some further description.

Positional Encoding

The positional encoding added to the encoder and decoder inputs is the first question mark in the model. What’s up with that?

Recall that the positional encoding is designed to help the model learn some notion of sequences and relative positioning of tokens. This is crucial for language-based tasks especially here because we are not making use of any traditional recurrent units.

In the Transformer architecture, the positional encoding is a vector described by the following equations:

$PE_{(pos,2i)} = \sin(\frac{pos}{10000^{2i/d_{model}}})$ $PE_{(pos,2i+1)} = \cos(\frac{pos}{10000^{2i/d_{model}}})$

Here the $i$ denotes the vector index we are looking at, $pos$ denotes the token, and $d_{model}$ denotes a fixed constant representing the dimension of the input embeddings. Ok let’s break it down further.

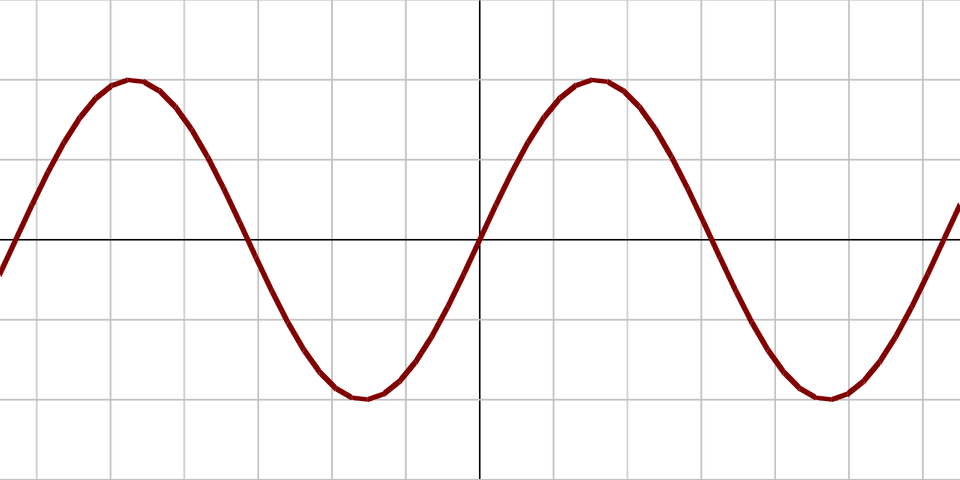
What this vector is basically saying is that for a given fixed vector index, as we vary the $pos$ (corresponding to tokens at different positions), we form a sinusoid:

This particular form for the positional encoding was chosen because the value for the encoding at a given position $PE_{pos+k}$ can be represented as a linear function of values for the encoding at earlier positions $PE_{pos}$. This follows from trigonometric identities and is equivalent to saying that a given token can learn to attend to earlier tokens in a sequence. This is an essential property for the Transformer.

Multi-head Attention

The multi-head attention operation is one of the main contributions of this model. So let’s dive into how it works.

At a high-level, an attention operation is designed to help a certain token in a natural language architecture focus on certain aspects of another part of the model, usually another collection of tokens. Keep in mind that attention operations can be used in other problem domains like computer vision, even though here we are focusing on natural language.

More formally, an attention takes a query, computes some weights with respect to a set of keys, and uses those weights to form a weighted combination of a collection of values. In mathematical terms, the Transformer attention can be described as:

$\textrm{Attention}(Q, K, V) = \textrm{softmax}(\frac{QK^T}{\sqrt{d_k}})V$

where $Q$, $K$, and $V$ are the query, key, and value matrices respectively and $d_k$ is a fixed scaling constant.

In the case of the encoder self-attention, the keys, values, and queries are all the same value, namely the output from the previous layer of encoding.

In the case of the masked decoder self-attention, the same is true except that a mask is applied so that a position of decoding can only attend to previous positions.

In the case of the encoder-decoder attention, the keys and values are the output of the encoder layer stack and the queries are the output of the previous decoder layer.

The multi-head attention operation basically means that instead of applying an attention operation once, we will do it several times (8 in the case of the Transformer model). Mathematically, this looks like:

$\textrm{MultiHead}(Q, K, V) = \textrm{Concatenate}(\textrm{head}_1, ..., \textrm{head}_h)W^O$ $\textrm{head}_i = \textrm{Attention}(QW_i^Q, KW_i^K, VW_i^V)$

where $W_{*}^{*}$ are appropriately-dimensioned weight matrices. The beauty of the multi-head attention is that the operation is easily parallelizable, which leads to reduced runtime.

Experiments

In spite of circumventing the traditional recurrent architectures, the Transformer is amazing because it is still able to outperform its recurrent counterparts. On the English-to-German and English-to-French WMT translation tasks, the Transformer achieves state-of-the-art BLEU scores (41.8 on EN-FR and 28.4 on EN-DE).

Not only that, but because of its highly parallelizable nature, the Transformer is able to do this at a significantly-reduced numbers of FLOPs (floating-point operations) for training! So the Transformer is better and faster!

Analysis

This whole notion of self-attention is an essential one in the Transformer architecture. It Why is self-attention a desirable thing to use as the backbone of a model?

One of the big advantages of self-attention is how efficient of an operation it is. A complexity comparison of self-attention to other conventional network operations illustrates this:

Layer Type	Layer Complexity	Sequential Operations
Self-Attention	$O(n^2\cdot d)$	$O(1)$
Recurrent	$O(n\cdot d^2)$	$O(n)$
Convolutional	$O(k\cdot n \cdot d^2)$	$O(1)$

Above, layer complexity denotes the number of computations performed per layer. In this case, self-attention is more efficient than recurrence as long as the sequence length $n$ is less than the input embedding dimension $d$, which is typically true.

The self-attention operation also connects all positions through a constant time number of computations, compared to recurrence which requires linear-time computations.

Final Thoughts

The Transformer is a real rebel in the natural language deep learning scene because of how it eschews conventional network constructs while still outperforming existing systems. It has challenged a lot of folk wisdom about the necessity of recurrence in natural language models. Since being released, the Transformer has been extended and used in new architectures, most recently BERT.

Is attention really all you need? Future work will answer that question!